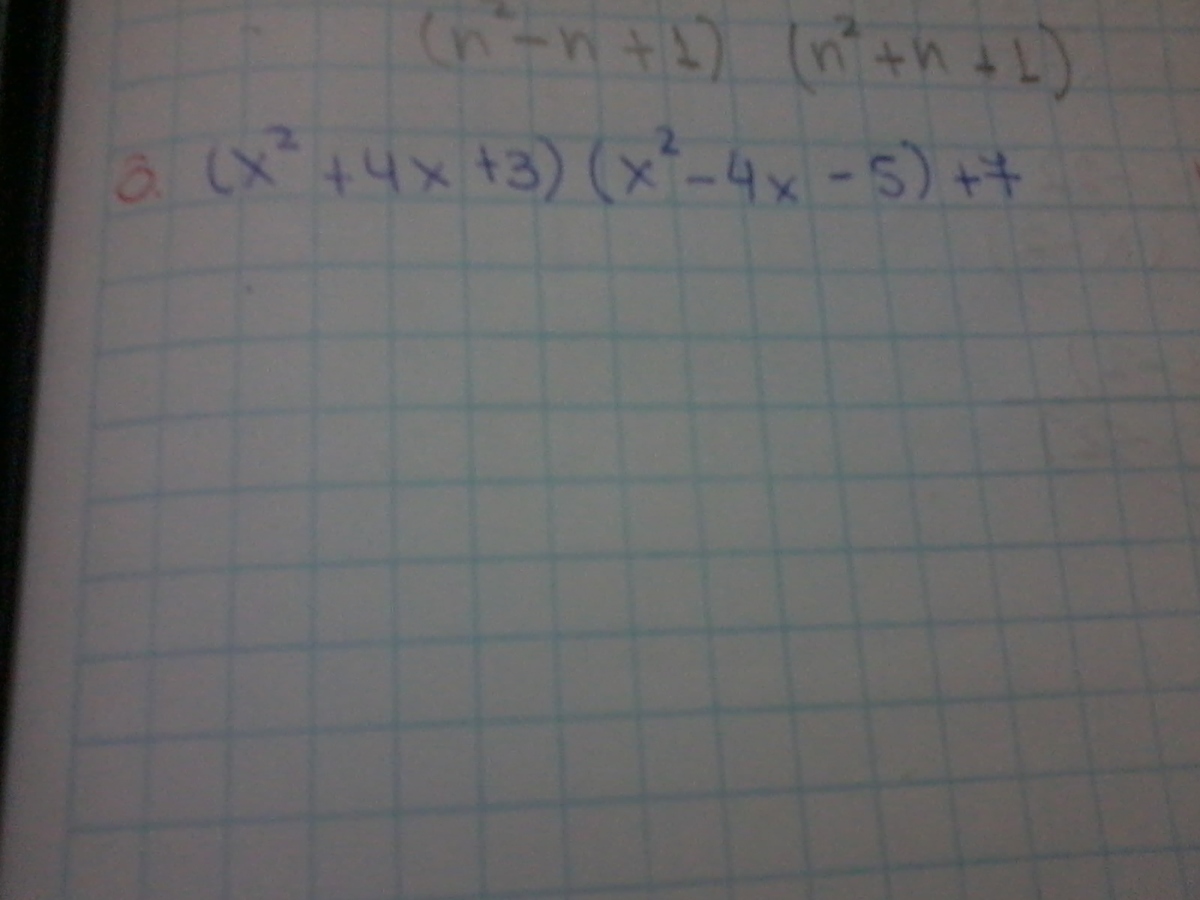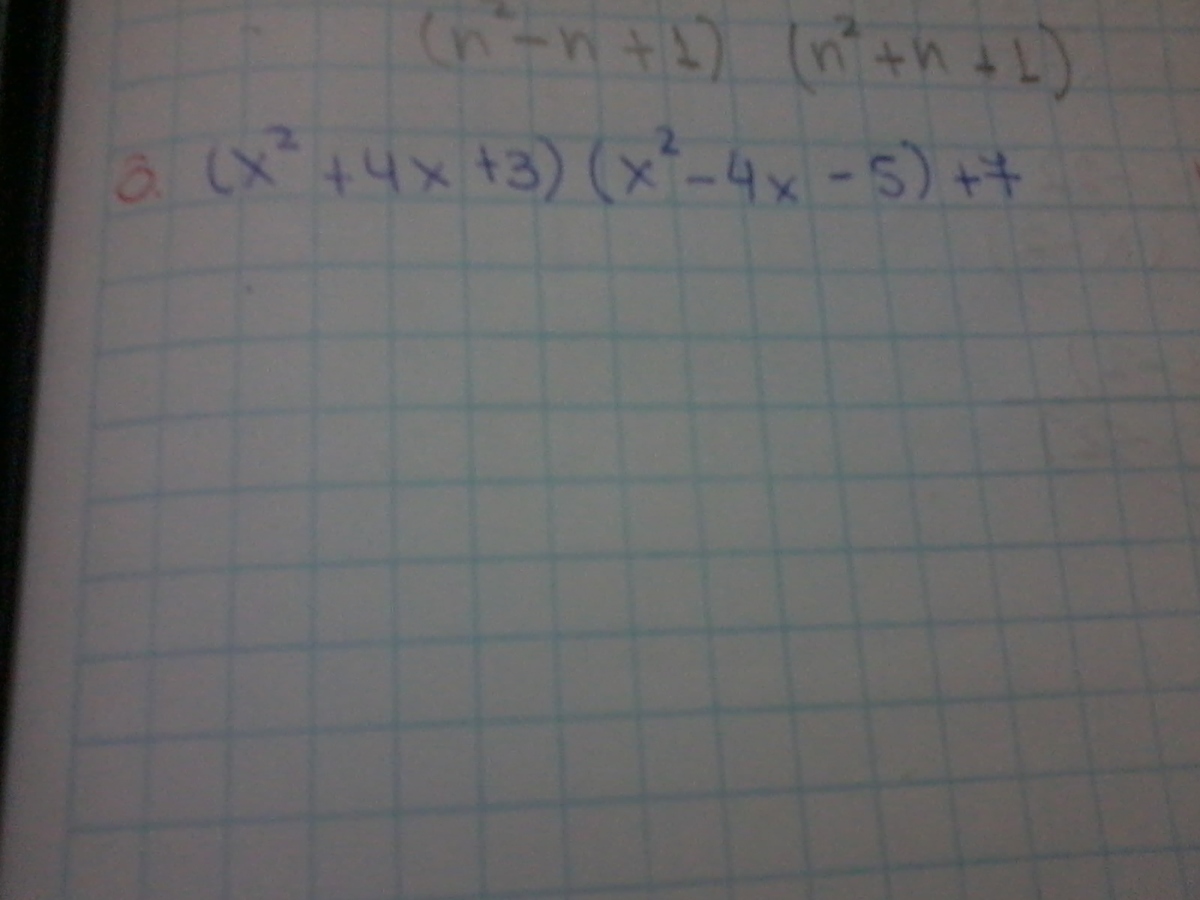Sagot :

Onikaminajidn
Sacar factor común: Es aplicar la propiedad distributiva de la multiplicación respecto de la suma, Así, la propiedad distributiva dice:  Pues bien, si nos piden factorizar la expresión , basta aplicar la propiedad distributiva y decir que  Cuando nos piden sacar factor común o simplemente factorizar y hay coeficientes con factores comunes, se saca el máximo común divisor de dichos coeficientes. Por ejemplo, si nos piden factorizar la expresión , será donde 6 es el máximo común divisor de 36, 12 y 18Para comprobar si la factorización se ha hecho correctamente, basta efectuar la multiplicación, aplicando la propiedad distributiva de la parte derecha de la igualdad, y nos tiene que dar la parte izquierda. Otro ejemplo: Factorizar   ¡Atención a cuando sacamos un sumando completo!, dentro del paréntesis hay que poner un uno. Tener en cuenta que si hubiéramos puesto  y quiero comprobar si está bien, multiplico y me da  pero no  como me tendría que haber dado.Sin embargo si efectúo  Otros ejemplos:  Si se trata de una diferencia de cuadrados: Es igual a suma por diferencia.Se basa en la siguiente fórmula  Pero aplicada al revés, o sea que si me dicen que factorice  escribo Otros ejemplos de factorización por este método:  Si se trata de un trinomio cuadrado perfecto: Es igual al cuadrado de un binomioSe basa en las siguientes fórmulas    y     Así si nos dicen que factoricemos: , basta aplicar la fórmula anterior y escribir que  Otros ejemplos de factorización por este método:  Si se trata de un trinomio de segundo grado: O sea un polinomio de este tipo, siendo a, b y c números Se iguala el trinomio a cero , se resuelve la ecuación , y si tiene dos soluciones distintas,  y se aplica la siguiente fórmula:  Veamos un ejemplo: Factorizar el polinomio Igualamos a cero Resolvemos la ecuación , y separando las dos soluciones , , y aplicando la fórmula, teniendo en cuenta que a=2  Para cualquier polinomio que tenga raíces enteras se puede aplicar la regla de Ruffini: Decir que un polinomio tienes raíces enteras es encontrar valores de x números enteros que al sustituirlos en el polinomio nos da cero. Si un polinomio de , por ejemplo, cuarto grado  tiene cuatro raíces enteras, , ,  y  se factoriza así:  Pero ¿cómo se obtienen las raíces?, por la regla de Ruffini Ejemplo: Factorizar Se aplica la regla de Ruffini, probando los divisores del término independiente, en este caso de 12. O sea que se prueba con 1, -1, 2, -2, 3, -3, 4, -4, 6, -6, 12 y –12 Probemos con unoSe copian los coeficientes del polinomio: 1-4-116-12  Y se escribe en una segunda línea el número uno   1-4-116-121            El primer coeficiente se copia abajo en una tercera línea  1-4-116-121      1     Se multiplica ese coeficiente, uno (1), por el número que estamos probando, en este caso también uno (1), o sea uno por uno = uno (1). Este uno se escribe debajo del siguiente coeficiente, o sea del –4  1-4-116-121 1    1    Se suma –4+1=-3  1-4-116-121 1    1-3   Se multiplica –3 por 1=-3 y se escribe debajo del siguiente coeficiente, -1   1-4-116-121 1-3   1-3   Se suma –3-1=-4 y así sucesivamente  1-4-116-121 1-3-412 1-3-4120Como vemos la última suma ha dado cero. Eso quiere decir que uno es una raíz del polinomio y que nos sirve para factorizar.Si hubiera dado distinto de cero habría que seguir probando los demás divisores de 12.Los coeficientes que han quedado en la última fila, en realidad son los coeficientes del cociente de dividir el polinomio entre x-1, y la última suma es el resto de dicha división.Si escribimos la relación fundamental de una división entera, o sea queDividendo=Divisor x Cociente+Resto == De hecho ya hemos factorizado el polinomio, pero el segundo factor de tercer grado hay que intentar seguir factorizando, de nuevo por la regla de Ruffini.Aplicando sucesivas veces esta regla queda:  1-4-116-121 1-3-412 1-3-41202 2-2-12  1-1-60 -2 -26   1-30   Como las raíces son, 1, 2 y –2 y el último cociente es x-3La factorización final es: =  Si en las sucesivas pruebas no encontramos ningún resto cero, quiere decir que el polinomio no se puede factorizar dentro de los números reales. 
solución:
1) (x^2 + 4x + 3) (x^2 - 4x -5) + 7 = (x^2 + 4x + 3) [(x^2 - 4x - 5 + 7)]
................................................ = (x^2 + 4x + 3) (x^2 - 4x + 2) Respuesta.

2) c^8(c^3 - 1) + c^4(c^3-1) + c^3 - 1 = (c^3 - 1) [ c^8 + c^4 + 1] Respuesta.

Espero haberte ayudado. Suerte.
Tu presencia en nuestra comunidad es crucial. Sigue haciendo preguntas y proporcionando respuestas. Juntos podemos construir una comunidad vibrante y enriquecedora. IDNStudies.com es tu fuente de respuestas confiables. Gracias por visitarnos y vuelve pronto para más información.